Chapter 5 Singular value decomposition

1. 奇异值分解(Singular value decomposition)

1.1 基础

矩阵的奇异值分解(SVD)提供了一种三项分解，类似于谱分解，但适用于任何矩阵。通过SVD，我们可以通过矩阵向量乘积$\bm{y} = \bm{Ax}$完整描述与$\bm{A}$相关的线性映射，其过程分为三步：首先对输入向量$\bm{x}$进行正交变换（旋转(rotation)或反射(reflection)）；然后对旋转后的输入向量的各元素进行非负缩放，并可能增加或移除该向量的维度以匹配输出空间的维度。最后，在输出空间中进行另一次正交变换。用公式表示为任意矩阵$\bm{A} \in \mathbb{R} ^{m,n}$都可以分解为

$$\bm{A} = \bm{U}\tilde{\bm{\Sigma}}\bm{V}^\top$$

其中$\bm{V} \in \mathbb{R} ^{n,n}$和$\bm{U} \in \mathbb{R} ^{m,m}$是正交矩阵（分别描述输入和输出空间中的旋转/反射），并且

$$\tilde{\bm{\Sigma}} = \begin{bmatrix} \Sigma & \bm{0}_{r,n-r} \\ \bm{0}_{m-r,r} & \bm{0}_{m-r,n-r} \end{bmatrix} , \Sigma = \operatorname{diag}(\sigma _1 ,\cdots ,\sigma _r) \succ 0$$

其中$r$是$\bm{A}$的秩，标量$\sigma _i > 0,i=1,\cdots ,r$，表示旋转输入向量上的缩放因子，如下图所示

$\bm{A}$的大部分相关特性都可以从其奇异值分解中推导出来。如果我们知道矩阵$\bm{A}$的SVD，那么我们也就知道了$\bm{A}$的秩、的谱范数（最大增益）以及条件数。此外，我们可以轻松获得$\bm{A}$的列空间和零空间的正交基；我们可以求解以$\bm{A}$为系数矩阵的线性方程组（参见Section第 6.4.2 节），并分析这些方程中误差的影响；我们还可以求解超定线性方程组的最小二乘解，或者欠定系统的最小范数解

1.2 奇异值分解定理

我们在这里陈述奇异值分解定理，并随后给出一个示意性证明

定理5.1（奇异值分解）：任何矩阵$\bm{A} \in \mathbb{R} ^{m,n}$都可以分解为

$$\bm{A} = \bm{U}\tilde{\bm{\Sigma}}\bm{V}^\top$$

其中$\bm{V} \in \mathbb{R} ^{n,n}$和$\bm{U} \in \mathbb{R} ^{m,m}$是正交矩阵（即$\bm{U}^\top \bm{U}=\bm{I}_m,\bm{V}^\top \bm{V}=\bm{I}_n$）并且$\tilde{\bm{\Sigma}}\in \mathbb{R} ^{m,n}$矩阵前$r \coloneqq \operatorname{rank} \bm{A}$个对角线元素$(\sigma _1,\cdots ,\sigma _r)$为正且按大小递减，其余所有元素为零

证明

考虑矩阵$\bm{A}^\top \bm{A} \in \mathcal{S}^n$。该矩阵是对称的且半正定，它可以进行谱分解

$$\bm{A}^\top \bm{A} = \bm{V \Lambda }_n \bm{V}^\top$$

其中$\bm{V} \in \mathbb{R} ^{n,n}$是正交矩阵（即$\bm{V}^\top \bm{V} = \bm{I}_n$），$\bm{\Lambda }_n$是对角矩阵，对角线上包含特征值$\lambda _i = \lambda _i(\bm{A}^\top \bm{A}) \geq 0,i=1,\cdots ,n$，按降序排列。由于$r = \operatorname{rank} \bm{A} = \operatorname{rank} \bm{A}^\top \bm{A}$，这些特征值中前$r$个是严格正的。注意$\bm{AA}^\top$和$\bm{A}^\top \bm{A}$具有相同的非零特征值，因此秩也都为$r$

1. $\operatorname{rank} \bm{A} = \operatorname{rank} \bm{A}^\top \bm{A}$

第一步：$\mathcal{N}(\bm{A}) \subseteq \mathcal{N}(\bm{A}^\top \bm{A})$

$\bm{Ax} = \bm{0} \Rightarrow \bm{A}^\top \bm{Ax} = \bm{0}$，证明完毕

第二步：$\mathcal{N}(\bm{A}^\top \bm{A}) \subseteq \mathcal{N}(\bm{A})$

$\bm{A}^\top \bm{Ax} = \bm{0} \Rightarrow \bm{x}^\top \bm{A}^\top \bm{Ax} = 0$，令$\bm{y} = \bm{Ax}$

$\bm{y}^\top \bm{y} = \lVert \bm{y} \rVert^2_2 = 0$，可得$\bm{y}=\bm{0}$，即$\bm{Ax}=\bm{0}$，证明完毕

第三步：秩的等式推导

最终有$\mathcal{N}(\bm{A}^\top \bm{A}) = \mathcal{N}(\bm{A})$，根据定理3.1知

$$\begin{gather*} \operatorname{rank} \bm{A} + \dim\mathcal{N}(\bm{A}) = n \\ \operatorname{rank} \bm{A}^\top \bm{A} + \dim\mathcal{N}(\bm{A}^\top \bm{A}) = n \end{gather*}$$

因此$\operatorname{rank} \bm{A} = \operatorname{rank} \bm{A}^\top \bm{A}$

同理可证$\operatorname{rank}\bm{A}^\top = \operatorname{rank} \bm{AA}^\top$，于是$\operatorname{rank}\bm{A}^\top = \operatorname{rank}\bm{A} = \operatorname{rank} \bm{AA}^\top = \operatorname{rank} \bm{A}^\top \bm{A}$

2. $\bm{A}^\top \bm{A}$的前$r$个特征值严格为正

实对称矩阵可正交对角化

$$\bm{V}^\top \bm{A}^\top \bm{AV} = \bm{\Lambda}_n = \operatorname{diag}(\lambda_1 ,\cdots , \lambda _n)$$

由于$\bm{V}$为正交矩阵，故其可逆。可知任何一个可逆矩阵都可以分解成一连串初等矩阵的乘积且初等变换不会改变矩阵的秩。因此$\bm{\Lambda}_n$的秩也为$r$，由于对角矩阵的秩为对角线上非零元素的个数，因此$\bm{A}^\top \bm{A}$的前$r$个特征值严格为正

3. $\bm{AA}^\top$与$\bm{A}^\top \bm{A}$有相同的非零特征值

第一步：若$\lambda$是$\bm{A}^\top \bm{A}$的非零特征值，则也是$\bm{AA}^\top$的特征值

根据特征值定义

$$\bm{A}^\top \bm{Ax} = \lambda \bm{x} ,\lambda \neq 0,\bm{x} \neq \bm{0}$$

两边左乘$\bm{A}$

$$\bm{AA}^\top \bm{Ax} = \lambda \bm{Ax}$$

令$\bm{y}=\bm{Ax}$

$$\bm{AA}^\top \bm{y} = \lambda \bm{y}$$

因为$\bm{y}\neq \bm{0}$，因此$\lambda$也是$\bm{AA}^\top$的特征值

第二步：若$\lambda$是$\bm{AA}^\top$的非零特征值，则也是$\bm{A}^\top \bm{A}$的特征值

证明过程同上

综上，$\bm{AA}^\top$与$\bm{A}^\top \bm{A}$非零特征值完全相同，仅特征值的重数可能因矩阵阶数不同而有差异因为$\bm{AA}^\top$和$\bm{A}^\top \bm{A}$的阶数不同

因此我们可以定义

$$\sigma _i \coloneqq \sqrt{\lambda_i(\bm{A}^\top \bm{A})} = \sqrt{\lambda _i(\bm{AA}^\top)} > 0 ,i=1,\cdots ,r$$

现在，将$\bm{V}$的前$r$列记为$\bm{v}_1,\cdots ,\bm{v}_r$，即$\bm{A}^\top \bm{A}$与$\lambda _1,\cdots ,\lambda _r$相关的特征向量。根据定义

$$\bm{A}^\top \bm{Av}_i = \lambda_i \bm{v}_i,i=1,\cdots ,r$$

因此，两边同时乘以$\bm{A}$

$$\bm{AA}^\top \bm{Av}_i = \lambda_i \bm{Av}_i,i=1,\cdots ,r$$

这意味着$\bm{Av}_i,i=1,\cdots,r$是$\bm{AA}^\top$的特征向量。这些特征向量是互相正交的，因为

$$\bm{v}_i^\top \bm{A}^\top \bm{Av}_j = \lambda _j \bm{v}_i^\top \bm{v}_j = \left\{ \begin{matrix} \lambda_i & \text{if }i=j \\ 0 & \text{otherwise} \end{matrix} \right.$$

因此，归一化向量

$$\bm{u}_i = \frac{\bm{Av}_i}{\sqrt{\lambda }_i} = \frac{\bm{Av}_i}{\sigma _i},i=1,\cdots ,r$$

形成一组与非零特征值$\lambda _1,\cdots ,\lambda _r$相关的标准正交向量集合。然后，对于$i=1,\cdots ,r$

$$\bm{u}_i^\top \bm{A} \bm{v}_j = \frac{1}{\sigma _i}\bm{v}_i^\top \bm{A}^\top\bm{A} \bm{v}_j = \frac{\lambda_j}{\sigma _i}\bm{v}_i^\top \bm{v}_j = \left\{ \begin{matrix} \sigma_i & \text{if }i=j \\ 0 & \text{otherwise} \end{matrix} \right.$$

用矩阵形式重写前面的关系可以得到

$$\begin{bmatrix} \bm{u}_1^\top \\ \vdots \\ \bm{u}_r^\top \end{bmatrix} \bm{A} \begin{bmatrix} \bm{v}_1 & \cdots & \bm{v}_r \end{bmatrix} = \operatorname{diag} (\sigma _1,\cdots ,\sigma_r) \coloneqq \Sigma$$

这已经是SVD的紧凑形式。接下来我们将推导SVD的完整版本。根据定义

$$\bm{A}^\top \bm{Av}_i = \bm{0},i=r+1,\cdots ,n$$

这意味着

$$\bm{Av}_i = \bm{0},i=r+1,\cdots ,n$$

为了验证后一种说法，通过反证法假设$\bm{A}^\top \bm{Av}_i = \bm{0}$且$\bm{Av}_i \neq \bm{0}$。则$\bm{Av}_i \in \mathcal{N}(\bm{A}^\top) \equiv \mathcal{R}(\bm{A})^\perp$，这是不可能的，因为显然$\bm{Av}_i \in \mathcal{R}(\bm{A})$。那么，我们可以找到正交单位向量$\bm{u}_{r+1},\cdots ,\bm{u}_m$使得$\bm{u}_1,\cdots ,\bm{u}_r,\bm{u}_{r+1},\cdots ,\bm{u}_m$构成$\mathbb{R} ^m$的一组正交基，那么

$$\bm{u}_i^\top \bm{A} \bm{v}_j = 0,i=1,\cdots ,m;j=r+1,\cdots ,n$$

综合两种情况，我们可以得到

$$\begin{bmatrix} \bm{u}_1^\top \\ \vdots \\ \bm{u}_m^\top \end{bmatrix} \bm{A} \begin{bmatrix} \bm{v}_1 & \cdots & \bm{v}_m \end{bmatrix} = \begin{bmatrix} \Sigma & \bm{0}_{r,n-r} \\ \bm{0}_{m-r,r} & \bm{0}_{m-r,n-r} \end{bmatrix} \coloneqq \tilde{\bm{\Sigma}}$$

定义正交矩阵$\bm{U} = [\bm{u}_1 ,\cdots ,\bm{u}_m]$ 后，表达式可重写为$\bm{U}^\top \bm{AV} = \tilde{\bm{\Sigma }}$，在左侧乘以$\bm{U}$、右侧乘以$\bm{V}^\top$后，最终得到完整的SVD分解

$$\bm{A} = \bm{U}\tilde{\bm{\Sigma}}\bm{V}^\top$$

$\bm{V}$由$\bm{A}^\top \bm{A}$的标准正交特征向量组成，因此$\bm{V} \in \mathbb{R} ^{n,n}$；$\bm{U}$由$\bm{AA}^\top$的标准正交特征向量组成，因此$\bm{U} \in \mathbb{R} ^{m,m}$

推论5.1（紧凑型SVD）：任何矩阵$\bm{A} \in \mathbb{R} ^{m,n}$都可以表示为

$$\bm{A} = \sum_{i=1}^{r} \sigma _i \bm{u}_i \bm{v}_i^\top = \bm{U}_r \Sigma \bm{V}_r^\top$$

其中$r = \operatorname{rank} \bm{A}$，$\bm{U}_r = [\bm{u}_1,\cdots ,\bm{u}_r]$满足$\bm{U}_r^\top \bm{U}_r = \bm{I}_r$，$\bm{V}_r = [\bm{v}_1,\cdots ,\bm{v}_r]$满足$\bm{V}_r^\top \bm{V}_r = \bm{I}_r$，并且$\sigma _1 \geq \sigma _2 \geq \cdots \sigma _r > 0$。正数$\sigma _i$称为$\bm{A}$的奇异值(singular value)，向量$\bm{u}_i$称为$\bm{A}$的左奇异向量(left singular vector)，$\bm{v}_i$称为右奇异向量(right singular vector)。这些量满足

$$\bm{Av}_i = \sigma _i \bm{u}_i, \bm{A}^\top \bm{u}_i^\top = \sigma _i \bm{v}_i, i = 1,\cdots,r$$

此外，$\sigma _i^2 = \lambda _i(\bm{AA}^\top ) = \lambda _i(\bm{A}^\top \bm{A} ),i=1,\cdots,r$且$\bm{u}_i$是$\bm{AA}^\top$的特征向量；$\bm{v}_i$是$\bm{A}^\top\bm{A}$的特征向量

2. 通过奇异值分解的矩阵性质

在本节中，我们回顾矩阵$\bm{A} \in \mathbb{R} ^{m,n}$的若干性质，这些性质可以直接从其完整形式的奇异值分解（SVD）中得出

$$\bm{A} = \bm{U}\tilde{\bm{\Sigma}}\bm{V}^\top$$

或紧凑形式的奇异值分解中得出

$$\bm{A} = \bm{U}_r\bm{\Sigma}\bm{V}^\top_r$$

2.1 秩、零空间和值域

矩阵$\bm{A}$的秩$r$是非零奇异值的数量，即$\tilde{\bm{\Sigma}}$对角线上非零元素的数量。此外，由于在实际中$\tilde{\bm{\Sigma}}$对角元素可能非常小但不完全为零（例如，存在数值误差），可以定义一个更可靠的数值秩，其定义为在给定容差$\epsilon \geq 0$的情况下，使$\sigma _k > \epsilon \sigma _1$的最大$k$

由于$r = \operatorname{rank} \bm{A}$，根据线性代数基本定理，$\bm{A}$的零空间的维数为$\dim \mathcal{N}(\bm{A}) = n − r$。一个跨越$\mathcal{N}(\bm{A})$的标准正交基由$\bm{V}$的最后$n-r$列给出，即

$$\mathcal{N}(\bm{A}) = \mathcal{R}(\bm{V}_{nr}),\bm{V}_{nr} \coloneqq [\bm{v}_{r+1},\cdots ,\bm{v}_n]$$

为了证明这一点，$\bm{v}_{r+1},\cdots ,\bm{v}_n$形成一个标准正交向量组（它们是一个正交矩阵的列）。此外，对于位于$\bm{V}_{nr}$范围内的任意向量$\bm{\xi} =\bm{V}_{nr} \bm{z}$，我们有

$$\bm{A \xi } = \bm{U}_r \Sigma \bm{V}_r^\top \bm{V}_{nr} \bm{z} = \bm{0}$$

类似地，$\bm{A}$值域的标准正交基由$\bm{U}$的前$r$列给出

$$\mathcal{R}(\bm{A}) = \mathcal{R}(\bm{U}_r),\bm{U}_r \coloneqq [\bm{u}_1,\cdots ,\bm{u}_r]$$

为了证明这一点，首先注意到，由于$\Sigma \bm{V}_r^\top \in \mathbb{R} ^{r,n}$，且$r \leq n$，是满行秩的，那么当$\bm{x}$遍历整个$\mathbb{R} ^n$空间时，$\bm{z} = \Sigma \bm{V}_r^\top \bm{x}$张成整个$\mathbb{R} ^r$空间，因此

$$\begin{align*} \mathcal{R}(\bm{A}) &= \left\{ \bm{y} \colon \bm{y} = \bm{Ax},\bm{x} \in \mathbb{R} ^n \right\} = \left\{ \bm{y} \colon \bm{y} = \bm{U}_r \Sigma \bm{V}_r^\top \bm{x},\bm{x} \in \mathbb{R} ^n \right\}\\ &= \left\{ \bm{y} \colon \bm{y} = \bm{U}_r \bm{z},\bm{z} \in \mathbb{R} ^r \right\} \equiv \mathcal{R}(\bm{U}_r) \end{align*}$$

2.2 矩阵范数

矩阵$\bm{A}\in \mathbb{R} ^{m,n}$Frobenius范数的平方可以定义为（乘以正交矩阵不会改变Frobenius范数）

$$\lVert \bm{A} \rVert _F^2 = \operatorname{trace} \bm{A}^\top \bm{A} = \sum_{i=1}^{n}\lambda _i(\bm{A}^\top \bm{A}) = \sum_{i=1}^{n} \sigma _i^2$$

其中$\sigma _i$是$\bm{A}$的奇异值。因此，Frobenius范数的平方是奇异值平方的和

矩阵谱范数平方等于$\bm{A}^\top \bm{A}$的最大特征值

$$\lVert \bm{A} \rVert _2^2 = \max_{\lVert \bm{u} \rVert_2=1}\lVert \bm{Au} \rVert _2^2 =\max_{\lVert \bm{u} \rVert_2=1} \bm{u}^\top \bm{A}^\top \bm{Au} = \sigma _1^2$$

也就是说，$\bm{A}$的谱范数与$\bm{A}$的最大奇异值相同

此外，矩阵$\bm{A}$的所谓核(nuclear)范数（也叫迹范数）是通过其奇异值来定义的

$$\lVert \bm{A} \rVert _* = \sum_{i=1}^{r} \sigma _i,r = \operatorname{rank} \bm{A}$$

可逆矩阵$\bm{A} \in \mathbb{R} ^{n,n}$的条件数(condition number)定义为其最大奇异值与最小奇异值的比值

$$\kappa(\bm{A})=\frac{\sigma_{1}}{\sigma_{n}}=\lVert \bm{A} \rVert_{2}\cdot \lVert \bm{A}^{-1} \rVert_{2}$$

这里逆矩阵的特征值可见下一节，该数值提供了$\bm{A}$接近奇异的量化衡量（$\kappa(\bm{A})$ 越大，A 越接近奇异）。条件数还提供了线性方程组解对方程系数变化的敏感性度量，参见第Section6.5节

2.3 矩阵伪逆(pseudoinverse)

给定任意矩阵$\bm{A} \in \mathbb{R} ^{m,n}$，令$r = \operatorname{rank} \bm{A}$，并对其进行SVD$\bm{A} = \bm{U}\tilde{\bm{\Sigma}}\bm{V}^\top$。所谓的Moore-Penrose伪逆（或广义逆(generalized inverse)）定义为

$$\bm{A}^\dagger = \bm{V}\tilde{\bm{\Sigma}}^\dagger\bm{U}^\top \in \mathbb{R} ^{n,m}$$

其中

$$\tilde{\bm{\Sigma}}^\dagger = \begin{bmatrix} \Sigma ^{-1} & \bm{0}_{r,m-r} \\ \bm{0}_{n-r,r} & \bm{0}_{n-r,m-r} \end{bmatrix}, \Sigma ^{-1} = \operatorname{diag} \left( \frac{1}{\sigma _1},\cdots, \frac{1}{\sigma }_r \right) \succ 0$$

上式也可以写出简洁形式

$$\bm{A}^\dagger = \bm{V}_r\bm{\Sigma}^{-1}\bm{U}_r^\top$$

根据定义有

$$\tilde{\bm{\Sigma}}^\dagger \tilde{\bm{\Sigma}} = \begin{bmatrix} \bm{I}_r & \bm{0}_{r,n-r} \\ \bm{0}_{n-r,r} & \bm{0}_{n-r,n-r} \end{bmatrix} , \tilde{\bm{\Sigma}}\tilde{\bm{\Sigma}}^\dagger = \begin{bmatrix} \bm{I}_r & \bm{0}_{r,m-r} \\ \bm{0}_{m-r,r} & \bm{0}_{m-r,m-r} \end{bmatrix}$$

由此伪逆具有以下性质

$$\begin{gather*} \bm{AA}^\dagger = \bm{U}_r\bm{U}_r^\top \\ \bm{A}^\dagger\bm{A} = \bm{V}_r\bm{V}_r^\top \\ \bm{AA}^\dagger\bm{A} = \bm{A} \\ \bm{A}^\dagger\bm{AA} ^\dagger = \bm{A}^\dagger \end{gather*}$$

注意以下三种特殊情况

1. 如果$\bm{A}$是方阵且非奇异，则$\bm{A}^\dagger = \bm{A}^{-1}$
2. 如果$\bm{A} \in \mathbb{R} ^{m,n}$列满秩，即$r = n \leq m$，那么此时$\bm{V}$为方阵，满足正交

$$\bm{A}^\dagger\bm{A} = \bm{V}_r\bm{V}_r^\top = \bm{V}\bm{V}^\top = \bm{I}_n$$

也就是说，在这种情况下，$\bm{A}^\dagger$是$\bm{A}$的左逆（即一个矩阵，当在左侧乘以$\bm{A}^\dagger$时，会得到单位矩阵：$\bm{A}^\dagger\bm{A} = \bm{I}_n$）。注意，在这种情况下$\bm{A}^\top \bm{A}$是可逆的，我们有

$$(\bm{A}^\top \bm{A})^{-1}\bm{A}^\top =(\bm{V}_r\bm{\Sigma}^{-2} \bm{V}^{\top}_r)\bm{V}_r\bm{\Sigma}^{\top}\bm{U}^{\top}_r =\bm{V}_r\bm{\Sigma}^{-2}\bm{\Sigma U}_{r}^{\top} = \bm{V}_r\bm{\Sigma}^{-1} \bm{U}_{r}^{\top} = \bm{A}^\dagger$$

$\bm{A}$的任何可能的左逆都可以表示为

$$\bm{A}^{li} = \bm{A}^\dagger + \bm{Q}^\top$$

其中$\bm{Q}$是某个矩阵，使得$\bm{A}^\top \bm{Q} = \bm{0}$（即$\bm{Q}$的列属于$\bm{A}^\top$的零空间）。综上所述，在列满秩的情况下，伪逆是$\bm{A}$的左逆，并且可以用$\bm{A}$写出出具体的表达式

$$\bm{A} \in \mathbb{R}^{m,n},r=\operatorname{rank}A = n\leq m \Rightarrow \bm{A}^\dagger \bm{A}=\bm{I}_n,\bm{A}^\dagger=(\bm{A}^\top \bm{A})^{-1}\bm{A}^\top$$

3. 如果$\bm{A} \in \mathbb{R} ^{m,n}$是行满秩，即$r = m \leq n$，那么此时$\bm{U}$为方阵，满足正交

$$\bm{AA}^\dagger = \bm{U}_r\bm{U}_r^\top = \bm{UU}^\top = \bm{I}_m$$

也就是说，在这种情况下，$\bm{A}^\dagger$是$\bm{A}$的右逆（即，当它在右侧与$\bm{A}$相乘时，会得到单位矩阵$\bm{AA}^\dagger = \bm{I}_m$）。注意，在这种情况下$\bm{AA}^\top$可逆，我们有

$$\bm{A}^\top(\bm{AA}^\top)^{-1} =\bm{V}_r \bm{\Sigma }^\top \bm{U}_r^\top (\bm{U}_r \bm{\Sigma}^{-2} \bm{U}_r^{\top})^\top = \bm{V}_r \bm{\Sigma }^{-1} \bm{U}_r^{\top} = \bm{A}^\dagger$$

$\bm{A}$的任何可能的右逆都可以表示为

$$\bm{A}^{ri} = \bm{A}^\dagger + \bm{Q}$$

其中$\bm{Q}$是某个矩阵，使得$\bm{A} \bm{Q} = \bm{0}$（即$\bm{Q}$的列属于$\bm{A}$的零空间）。综上所述，在行满秩的情况下，伪逆是$\bm{A}$的右逆，并且可以用$\bm{A}$写出出具体的表达式

$$\bm{A} \in \mathbb{R}^{m,n},r=\operatorname{rank}A = m\leq n \Rightarrow \bm{AA}^\dagger = \bm{I}_m,\bm{A}^\dagger=\bm{A}^\top(\bm{AA}^\top)^{-1}$$

2.4 正交投影算子

我们已经看到，任何矩阵$\bm{A} \in \mathbb{R} ^{m,n}$都定义了输入空间$\mathbb{R} ^n$与输出空间$\mathbb{R} ^m$ 之间的线性映射$\bm{y} = \bm{Ax}$。此外，根据线性代数的基本定理，输入空间和输出空间可分解为正交分量，如下所示

$$\begin{gather*} \mathbb{R}^n = \mathcal{N}(\bm{A}) \oplus \mathcal{N}(\bm{A})^\perp = \mathcal{N}(\bm{A}) \oplus \mathcal{R}(\bm{A}^\top) \\ \mathbb{R}^m = \mathcal{R}(\bm{A}) \oplus \mathcal{R}(\bm{A})^\perp = \mathcal{R}(\bm{A}) \oplus \mathcal{N}(\bm{A}^\top) \end{gather*}$$

如前所述，SVD$\bm{A} = \bm{U}\tilde{\bm{\Sigma}}\bm{V}^\top$为这四个子空间提供了标准正交基

$$\bm{U} = [\bm{U}_r \quad \bm{U}_{nr}],\bm{V} = [\bm{V}_r \quad \bm{V}_{nr}]$$

其中$\bm{U}_r,\bm{V}_r$分别包含$\bm{U}$和$\bm{V}$的前$r = \operatorname{rank} \bm{A}$列，我们有

$$\begin{gather*} \mathcal{N}(\bm{A}) = \mathcal{R}(\bm{V}_{nr}), \mathcal{N}(\bm{A})^\perp \equiv \mathcal{R}(\bm{A}^\top ) = \mathcal{R}(\bm{V}_r) \\ \mathcal{R}(\bm{A}) = \mathcal{R}(\bm{U}_{r}), \mathcal{R}(\bm{A})^\perp \equiv \mathcal{N}(\bm{A}^\top ) = \mathcal{R}(\bm{U}_{nr}) \end{gather*}$$

接下来我们讨论如何计算向量$\bm{x} \in \mathbb{R} ^n$在$\mathcal{N}(\bm{A}),\mathcal{N}(\bm{A})^\perp$上的投影，以及向量$\bm{y} \in \mathbb{R} ^m$在$\mathcal{R}(\bm{A}),\mathcal{R}(\bm{A})^\perp$上的投影

首先，我们回顾一下，给定一个向量$\bm{x} \in \mathbb{R} ^n$和$d$个线性无关的向量$\bm{b}_1,\cdots ,\bm{b}_d \in \mathbb{R} ^n$，$\bm{x}$在由$\left\{ \bm{b}_1,\cdots ,\bm{b}_d \right\}$张成的子空间上的正交投影是向量

$$\bm{x}^* = \bm{B \alpha }$$

其中$\bm{B} =[\bm{b}_1,\cdots ,\bm{b}_d ]$而$\bm{\alpha }$需要通过解线性方程组得到

$$\bm{B}^\top \bm{B \alpha } = \bm{B}^\top \bm{x}$$

上述方程请参考Section2.3节。特别注意，如果$\bm{B}$中的基向量是标准正交的（注意此时$\bm{B}$并不一定是方阵，因此它并不一定是正交矩阵），那么有$\bm{B}^\top \bm{B} = \bm{I}_d$，因此线性方程组有一个直接解$\bm{\alpha } = \bm{B}^\top \bm{x}$，投影可以简单地计算为$\bm{x}^* = \bm{BB}^\top \bm{x}$

回到我们感兴趣的情况，设$\bm{x} \in \mathbb{R} ^n$，并且假设我们想要计算$\bm{x}$在$\mathcal{N}(\bm{A})$上的投影。由于$\mathcal{N}(\bm{A})$的一组标准正交基由$\bm{V}_{nr}$的列给出，根据前面的推理，我们可以立即得到

$$[\bm{x}]_{\mathcal{N}(\bm{A})} = (\bm{V}_{nr}\bm{V}_{nr}^\top )\bm{x}$$

我们使用符号$[\bm{x}]_{\mathcal{S}}$来表示向量$\bm{x}$在子空间$\mathcal{S}$上的投影。现在，注意到

$$\bm{I}_n = \bm{VV}^\top = \bm{V}_r \bm{V}_r^\top + \bm{V}_{nr} \bm{V}_{nr}^\top$$

因此

$$P_{\mathcal{N}(\bm{A})} = \bm{V}_{nr} \bm{V}_{nr}^\top = \bm{I}_n - \bm{V}_r \bm{V}_r^\top = \bm{I}_n - \bm{A}^\dagger \bm{A}$$

矩阵$P_{\mathcal{N}(\bm{A})}$被称为投影到子空间$\mathcal{N}(\bm{A})$的正交投影算子。在$\bm{A}$为行满秩的特殊情况下，$\bm{A}^\dagger = \bm{A}^\top(\bm{AA}^\top)^{-1}$，那么

$$P_{\mathcal{N}(\bm{A})} = \bm{I}_n - \bm{A}^\top(\bm{AA}^\top)^{-1}\bm{A},\quad \bm{A} \text{为行满秩}$$

通过类似的推理，我们得到$\bm{x} \in \mathbb{R} ^n$在$\mathcal{N}(\bm{A})^\perp \equiv \mathcal{R}(\bm{A}^\top )$上的投影由下式给出

$$[\bm{x}]_{\mathcal{N}(\bm{A})^\perp } = (\bm{V}_{r}\bm{V}_{r}^\top )\bm{x} = P_{\mathcal{N}(\bm{A})^\perp }\bm{x},P_{\mathcal{N}(\bm{A})^\perp } = \bm{A}^\dagger \bm{A}$$

特殊情况下

$$P_{\mathcal{N}(\bm{A})^\perp } = \bm{A}^\top(\bm{AA}^\top)^{-1}\bm{A},\quad \bm{A} \text{为行满秩}$$

类似地，对于$\bm{y} \in \mathbb{R} ^m$，我们有

$$\begin{gather*} [\bm{y}]_{\mathcal{R}(\bm{A})} = (\bm{U}_{r}\bm{U}_{r}^\top )\bm{y} = P_{\mathcal{R}(\bm{A})} \bm{y} , P_{\mathcal{R}(\bm{A})} = \bm{AA}^\dagger \\ P_{\mathcal{R}(\bm{A})} = \bm{A}(\bm{A}^\top \bm{A})^{-1}\bm{A}^\top ,\quad \bm{A} \text{为列满秩} \\ [\bm{y}]_{\mathcal{R}(\bm{A})^\perp } = (\bm{U}_{nr}\bm{U}_{nr}^\top )\bm{y} = P_{\mathcal{R}(\bm{A})^\perp } \bm{y} , P_{\mathcal{R}(\bm{A})^\perp} =\bm{I}_m- \bm{AA}^\dagger \\ P_{\mathcal{R}(\bm{A})^\perp} = \bm{I}_m- \bm{A}(\bm{A}^\top \bm{A})^{-1}\bm{A}^\top ,\quad \bm{A} \text{为列满秩} \end{gather*}$$

子空间上的投影。我们考虑计算给定向量$\bm{y} \in \mathbb{R} ^m$投影到由给定向量集$\mathcal{S} = \operatorname{span}(\bm{a}^{(1)},\cdots , \bm{a}^{(n)}) \subseteq \mathbb{R} ^m$所生成子空间的问题，正如在第Section 2.3 节和第 5.2 节中已经讨论的那样。显然，$\mathcal{S}$与将这些向量作为列的矩阵$\bm{A} \coloneqq [\bm{a}^{(1)},\cdots , \bm{a}^{(n)}]$的列空间相一致，因此我们面临的问题是

$$\min_{\bm{z} \in \mathcal{R}(\bm{A})} \lVert \bm{z} - \bm{y} \rVert _2$$

如果$r \coloneqq \operatorname{dim} \mathcal{S} = \operatorname{rank} (\bm{A})$，那么$\bm{A}$的紧凑形式奇异值分解为$\bm{A} = \bm{U}_r\bm{\Sigma}\bm{V}^\top_r$，并且上式的唯一最小范数解由投影定理给出为

$$\bm{z}^* = [\bm{y}]_{\mathcal{S}} = P_{\mathcal{R}(\bm{A})}\bm{y} = \bm{AA}^\dagger \bm{y} = ( \bm{U}_r\bm{U}_r^\top) \bm{y}$$

其中$P_{\mathcal{R}(\bm{A})}$是到$\mathcal{R}(\bm{A})$的正交投影算子。注意到投影$\bm{z}^*$是$\bm{y}$的线性函数，并且定义该投影的矩阵由$\bm{A}$SVD的$\bm{U}_r$因子提供

类似地，假设我们想要找到$\bm{y}$在$\mathcal{S}^\perp$上的投影，即$\mathcal{S}$的正交补。由于$\mathcal{S}^\perp = \mathcal{N}(\bm{A}^\top )$，该问题可写为

$$\min_{\bm{z} \in \mathcal{N}(\bm{A}^\perp )} \lVert \bm{z} - \bm{y} \rVert _2$$

方程的解为

$$\bm{z}^* = [\bm{y}]_{\mathcal{S}^\perp } =(\bm{I}_m - \bm{AA}^\dagger )\bm{y}$$

3. 奇异值分解与优化

在本节中，我们将说明如何通过奇异值分解方便地解决某些优化问题。SVD在优化中的进一步应用将在Section第六章中介绍

3.1 低秩矩阵近似(Low-rank matrix approximations)

设$\bm{A} \in \mathbb{R} ^{m,n}$是一个给定矩阵，且$\operatorname{rank}(\bm{A}) = r > 0$。这里我们考虑用低秩矩阵近似$\bm{A}$的问题。具体来说，我们考虑以下秩受限近似问题

$$\begin{gather*} \min _{\bm{A}_k \in \mathbb{R} ^{m,n}} \lVert \bm{A} - \bm{A}_k \rVert _F^2 \\ \text{s.t. :}\operatorname{rank}(\bm{A}_k) = k \end{gather*}$$

其中$1 \leq k \leq r$是给定的。令

$$\bm{A} = \bm{U}\tilde{\Sigma}\bm{V}^\top = \sum_{i=1}^{r}\sigma _i \bm{u}_i \bm{v}_i^\top$$

为$\bm{A}$的SVD。接下来我们将证明，上述问题的最优解可以通过将前面的求和截断到第$k$项来简单获得，即

$$\bm{A}_k = \sum_{i=1}^{k}\sigma _i \bm{u}_i \bm{v}_i^\top$$

为了证明上述低秩近似结果，注意到Frobenius范数是幺正不变(unitarily
invariant)的，这意味着对于所有$\bm{Y} \in \mathbb{R} ^{m,n}$以及任意正交矩阵$\bm{Q} \in \mathbb{R} ^{m,n},\bm{R} \in \mathbb{R} ^{m,n}$，都有$\lVert \bm{Y} \rVert_F = \lVert \bm{QYR} \rVert_F$。因此

$$\lVert \bm{A} - \bm{A}_k \rVert^2_F = \lVert \bm{U}^\top ( \bm{A} - \bm{A}_k V) \rVert^2_F = \lVert \tilde{\Sigma} - \bm{Z} \rVert^2_F$$

其中$\bm{Z} = \bm{U}^\top \bm{A}_k \bm{V}$，通过变量变换，问题可以表述为

$$\begin{gather*} \min _{\bm{Z} \in \mathbb{R} ^{m,n}} \left\lVert \begin{bmatrix} \operatorname{diag}(\sigma _1,\cdots ,\sigma _r) & \bm{0}_{r,n-r} \\ \bm{0}_{m-r,r} & \bm{0}_{m-r,n-r} \end{bmatrix}-\bm{Z} \right\rVert _F^2 \\ \text{s.t. :}\operatorname{rank}(\bm{Z}) = k \end{gather*}$$

注意，初等变换不会改变矩阵的秩。可以假设$\bm{Z}$是对角矩阵，因为考虑$\bm{Z}$中的非零非对角元素只会使该问题中的Frobenius范数目标变差。因此，目标变为

$$f_0 = \lVert \operatorname{diag}(\sigma _1,\cdots ,\sigma _r) - \operatorname{diag}(z_1,\cdots ,z_r) \rVert _F^2 = \sum_{i=1}^{r}(\sigma _i - z_i)^2$$

由于约束条件$\operatorname{rank}(\bm{Z}) = k$要求对角线上恰好$k$个元素$z_i$非零，最好的选择是设置$z_i = \sigma _i,i = 1,\cdots ,k$并且$z_i =0,i>k$。通过这种方式，前$k$个$z_i$中和了A的最大奇异值，使得目标中的剩余项仅包含$r-k$个最小奇异值，即一个最优解为

$$\bm{Z}^* = \begin{bmatrix} \operatorname{diag}(\sigma _1,\cdots ,\sigma _k,0,\cdots ,0) & \bm{0}_{r,n-r} \\ \bm{0}_{m-r,r} & \bm{0}_{m-r,n-r} \end{bmatrix}$$

最优的目标为

$$f_0^* = \sum_{i=k+1}^{r} \sigma _i^2$$

原问题的最优解可以通过变量变换$\bm{Z} = \bm{U}^\top \bm{A}_k \bm{V}$恢复，得到

$$\bm{A}_k = \bm{U} \bm{Z}^* \bm{V}^\top = \sum_{i=1}^{k} \sigma _i \bm{u}_i \bm{v}_i^\top$$

这确实与我们猜测的一致。按照完全相同的推理，我们实际上可以证明，这个解不仅对于Frobenius范数目标是最优的，对于谱矩阵范数（最大奇异值）也是最优的。也就是说，$\bm{A}_k$对于以下问题也是最优的（谱范数同样是幺正不变的）

$$\begin{gather*} \min _{\bm{A}_k \in \mathbb{R} ^{m,n}} \lVert \bm{A} - \bm{A}_k \rVert _2^2 \\ \text{s.t. :}\operatorname{rank}(\bm{A}_k) = k \end{gather*}$$

比率

$$\eta _k = \frac{\lVert \bm{A}_k \rVert_F^2}{\lVert \bm{A}\rVert_F^2} = \frac{\sigma _1^2 + \cdots + \sigma _k^2}{\sigma _1^2 + \cdots + \sigma _r^2}$$

表示$\bm{A}$的秩为$k$的近似在多大程度上解释了$\bm{A}$的总方差（Frobenius范数）。显然，$\eta _k$与相对范数近似误差有关

$$e_k = \frac{\lVert \bm{A} - \bm{A}_k \rVert_F^2}{\lVert \bm{A}\rVert_F^2} = \frac{\sigma _{k+1}^2 + \cdots + \sigma _r^2}{\sigma _1^2 + \cdots + \sigma _r^2} = 1 - \eta _k$$

备注5.2（到秩亏的最小距离）：假设$\bm{A}\in \mathbb{R} ^{m,n},m \leq n$，且满秩，即$\operatorname{rank}(\bm{A}) = n$。我们想知道使$\bm{A} +\bm{\delta A}$变为秩亏（非满秩）的最小扰动$\bm{\delta A}$。最小扰动的Frobenius范数（或谱范数）衡量了$\bm{A}$到秩亏的距离。形式上，我们需要解

$$\begin{gather*} \min _{\bm{\delta A} \in \mathbb{R} ^{m,n}} \lVert \bm{\delta A}\rVert _F^2 \\ \text{s.t. :}\operatorname{rank}(\bm{A} + \bm{\delta A}) = n-1 \end{gather*}$$

这个问题等价于低秩矩阵近似，其中$\bm{\delta A} = \bm{A}_k - \bm{A}$。因此解可以很容易得到为

$$\bm{\delta A}^* = \bm{A}_k -\bm{A}$$

其中$\bm{A} = \sum_{i=1}^{n}\sigma _i \bm{u}_i \bm{v}_i^\top$是$\bm{A}$的紧凑型奇异值分解并且$\bm{A}_k = \sum_{i=1}^{n-1}\sigma _i \bm{u}_i \bm{v}_i^\top$，因此，我们有

$$\bm{\delta A}^* = -\sigma _n \bm{u}_n \bm{v}_n^\top$$

这个结果表明，导致秩亏的最小扰动是一个秩为一的矩阵，而且到秩亏的距离为$\lVert \bm{\delta A}^* \rVert_F = \lVert \bm{\delta A}^* \rVert_2 = \sigma _n$

3.2 主成分分析(Principal component analysis)

主成分分析是一种无监督学习技术，广泛用于发现数据集中最重要或最具信息量的方向，也就是数据变化最大方向

考虑下图中的二维数据云：沿着大约45度方向几乎包含了数据的所有变化。相比之下，沿着大约135度方向包含的数据变化很少。这意味着，在这个例子中，数据背后的重要现象本质上沿着45度的方向是一维的。当分析维度大于3的数据时，图形直觉就无济于事，这时主成分分析就显得很有用

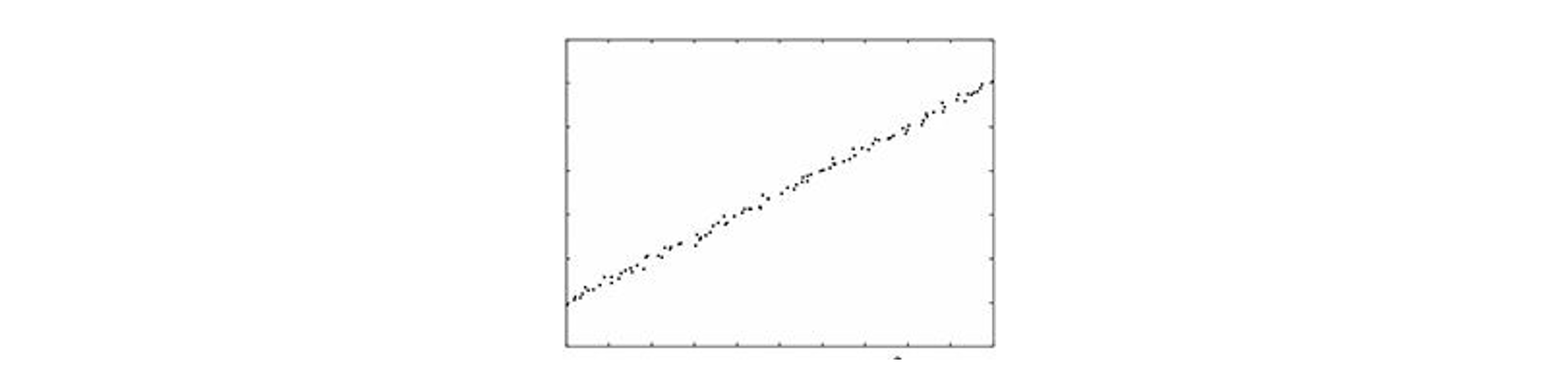
设$\bm{x}_i \in \mathbb{R} ^n,i=1,\cdots ,m$为希望分析的给定数据点，记数据点的平均值为$\bar{\bm{x}} = \frac{1}{m} \sum_{i=1}^{m}\bm{x}_i$，并设$\tilde{\bm{X}}$是$n \times m$阶矩阵并包含居中后的数据点

$$\tilde{\bm{X}} = [\tilde{\bm{x}}_1 \quad \cdots \tilde{\bm{x}}_m],\tilde{\bm{x}}_i \coloneqq \bm{x}_i - \bar{\bm{x}},i=1,\cdots ,m$$

我们在数据空间中寻找一个归一化方向$\bm{z} \in \mathbb{R} ^n$，满足$\lvert \bm{z} \rvert^2 = 1$，使得中心化数据点在由$\bm{z}$决定的直线上的投影方差最大。我们选择在 $\bm{z}$的归一化中使用欧几里得范数，是因为它不会偏向任何特定方向

沿$\bm{z}$方向的中心化数据的分量由下式给出（参见Section例如第 2.3.1 节）

$$\alpha _i = \tilde{\bm{x}}_i^\top \bm{z},i=1,\cdots ,m$$

注意，αi z 是 i 在 z 的张成空间上的投影。沿着方向 z 的数据均方变化由此给出

---

未完待续